深入理解索引
-
索引基础理论知识
-
B+树索引
-
哈希索引
-
理解B+树,哈希索引结构及区别
-
理解常见索引的基本概念:主键索引,唯一索引,普通索引,联合索引之间的区别
-
理解MyISAM和InnoDB的索引结构区别
-
理解如何通过索引提高SQL效率
binary search, 二分查找法,也叫折半查找(折半搜索,二分查找算法,二分搜索),是一种再有序数组中查找某一特定元素的搜索算法。
这种搜索算法每一次比较都使搜索范围减小一般,可在最坏的情况下用0(log n)完成搜索任务。
二分查找法的优点是比较次数少,查找速度块,平均性能好
缺点是要求待查表为有序表,且插入删除困难。
因此,折半查找方法适用于不经常变动而查找频繁的有序列表
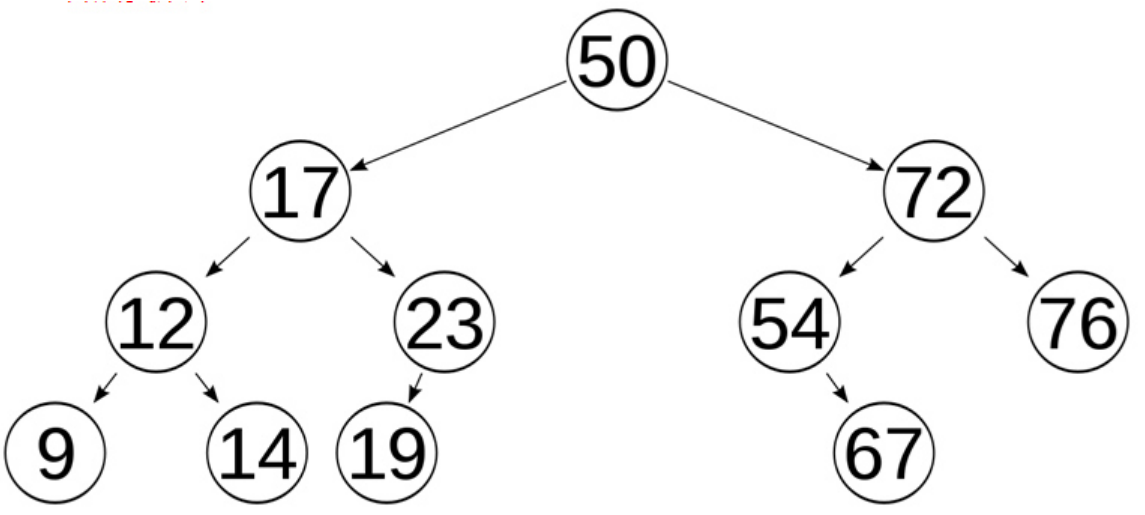
binary tree, 二叉树
每个节点至多只有两颗子树(不存在度大于2的节点),二叉树的子树有左右有序之分,次序不能颠倒
平衡二叉树
-
左右两个字数的高度差的绝对值不会大过1(<=1),且左右两个子树也是平衡二叉树
-
不平衡树会通过自旋,变成平衡树
-
平衡树和二叉查找的最大区别:前者是平衡的,后者未必

旋转后

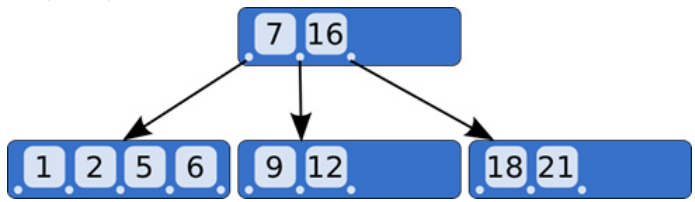
用下面这些值来构造一个B树
ACGHEKQMFWLTZDPRXYS
1.构造一个4阶的B树,非根节点关键字数,小于2个就合并,大于4个就分裂
2.插入H
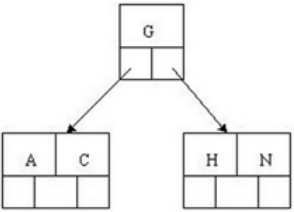
3.插入E,K,Q时不需要任何分裂操作,变成:
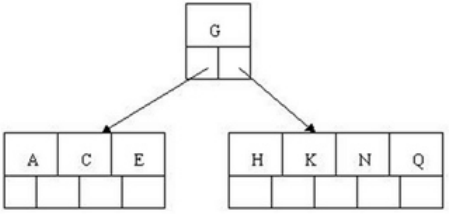
4.插入M之后就需要分裂了,M恰好时中间关键字元素,可以放在根节点
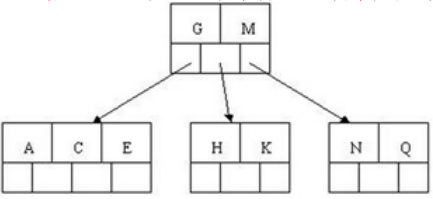
5.插入F,W,L,T不需要任何分裂操作
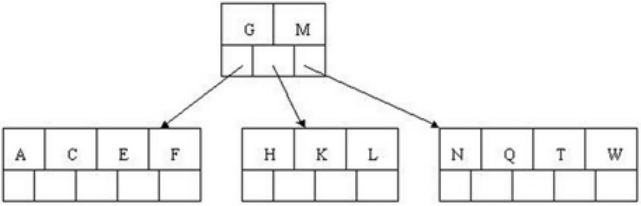
6.插入Z时,最右边的叶子节点空间满了,需要进行分裂操作,中间元素T上移到父节点中
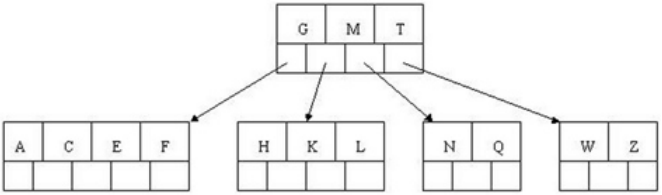
7.插入D时,导致最左边的叶子节点被分裂,D是中间元素,上移到父节点
8.最后,当插入S时,第三个子节点需要分裂,但根节点已经满了,需要把根节点再次分裂,形成3层的B树
再来看下元素的删除
1.删除H,节点无需进行合并或分裂
2.删除T之后,最右边的子节点就没有父节点了,需要再找个新的元素放在其父节点

3.删除R
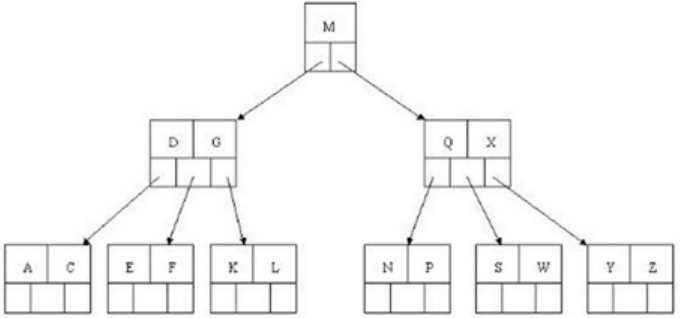
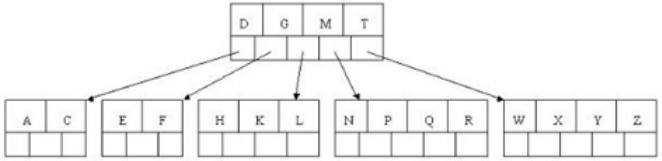
4.删除E之后,第一步变成了
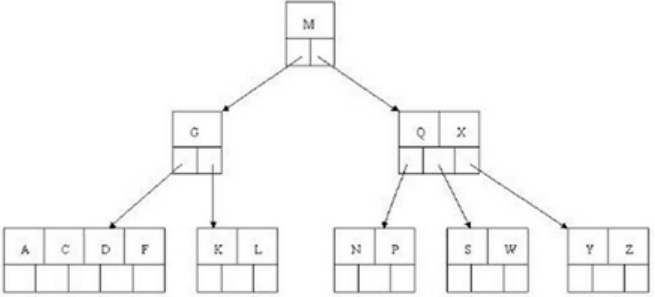
可以把G,M,Q,X这4个元素提升到根节点,变成了
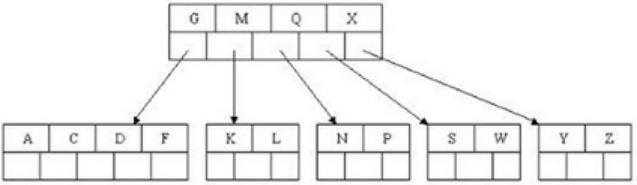
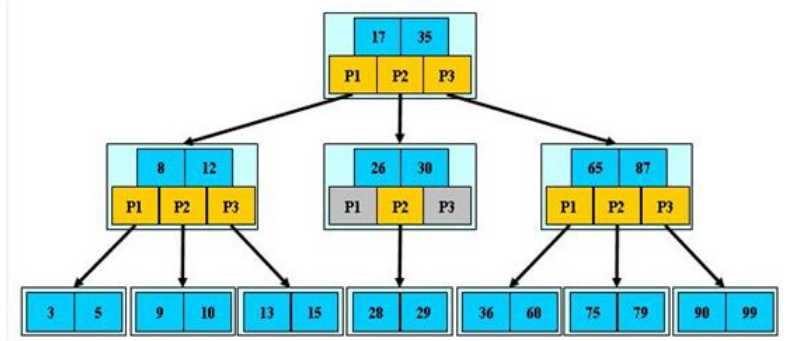
B+树是B树(B Tree)的变体,也是一种多路搜索树
-
非叶子节点的子树指针与关键字个数相同
-
为所有叶子节点增加一个链指针
-
所有关键字都在叶子节点出现
二叉树,B树,B+树的小结
Binary树:二叉树,每个节点之存储一个关键字,等于则命中,小于则走左节点,大于走右节点
B树:多路搜索树,没个节点存储M/2到M个关键字,非叶子节点存储指向关键字范围的子节点
所有关键字在整颗树中出现,且只出现一次,非叶子节点可以命中
B+树:在B-树基础上,为叶子节点增加链表指针,所有关键字都在叶子节点中出现,非叶子节点左右叶子节点的索引,B+树总是到叶子节点才命中
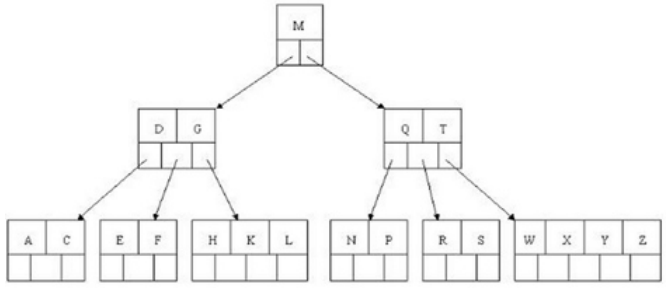
经典B+树结构
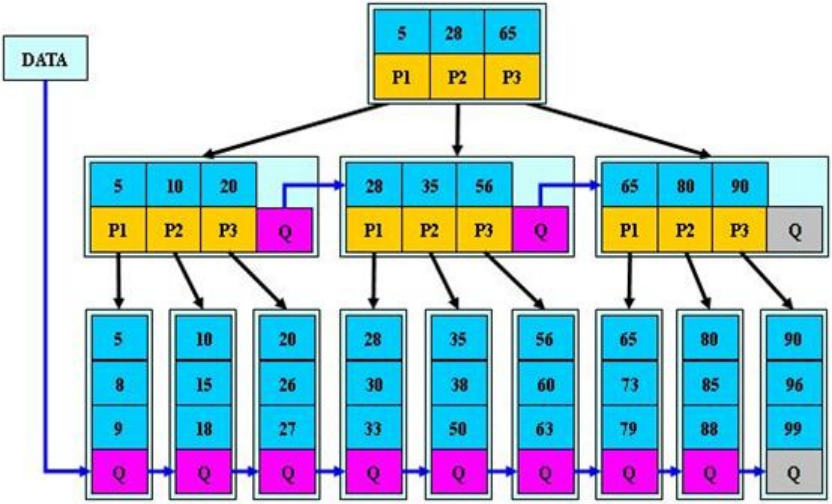
==========================================
B+树插入新元素时,可能会遇到3种情况

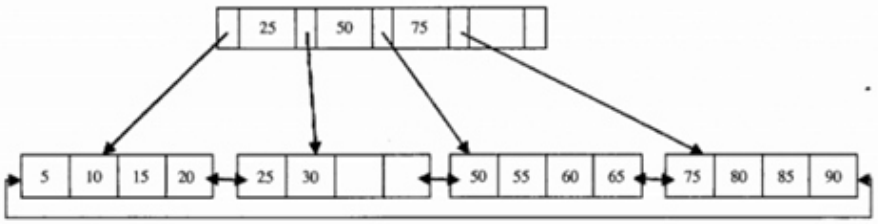
-
插入元素28(直接写入 叶子节点没有满)
-
插入元素70
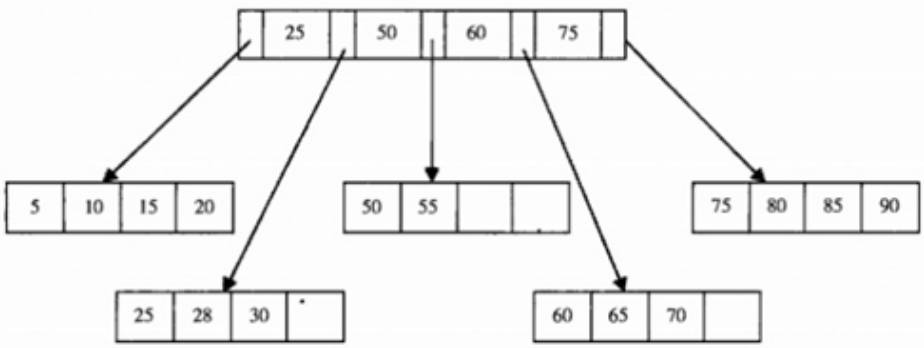
3.插入元素95
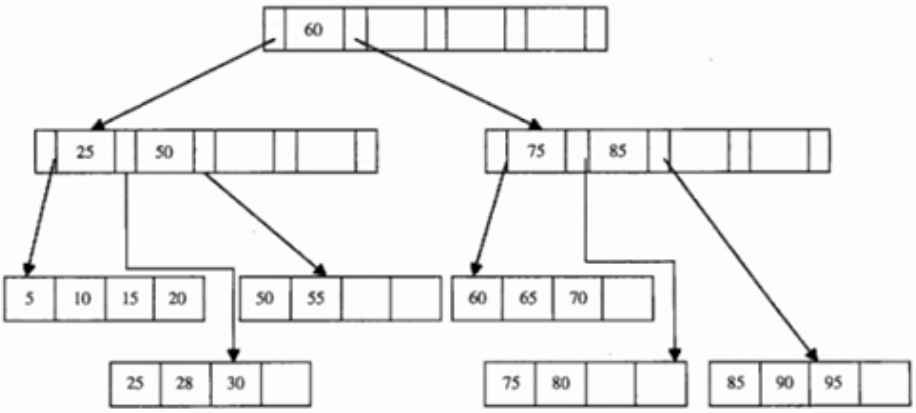
B+树删除元素时,也可能遇到3中情况

-
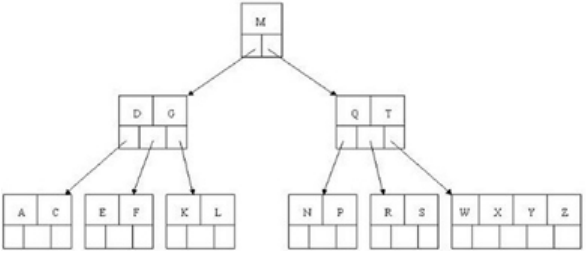
从这个B+树中删除元素70,变成了
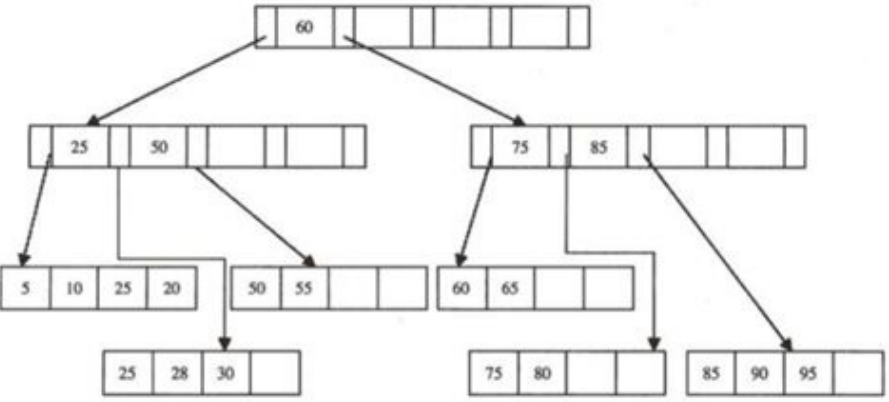
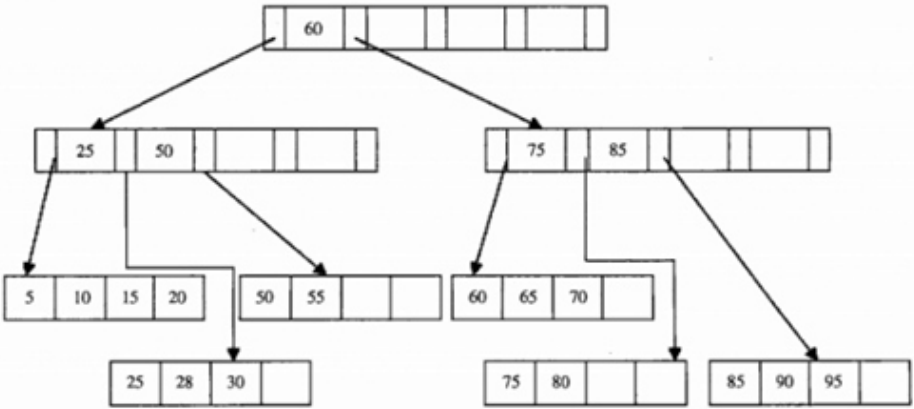
2.再删除元素25,变成了:

3.再删除元素60,变成了:
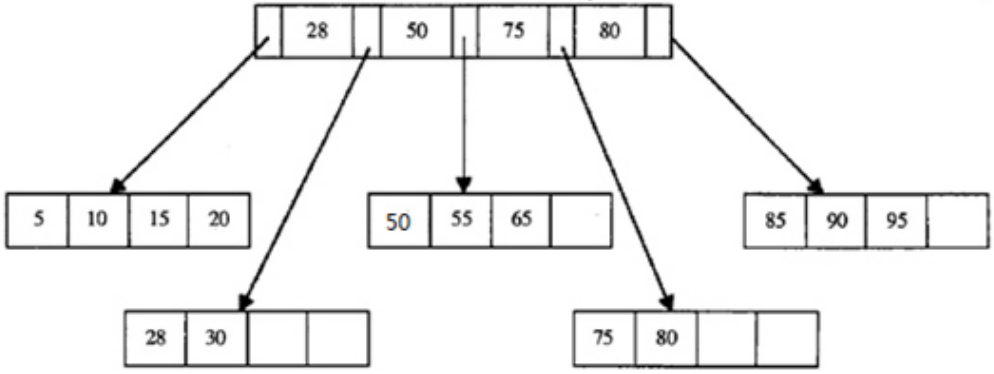
用Innodb的时候一定要注意
-
要用顺序自增的主键
-
主键可以删除(也不建议)但是一定不要更新它,更新后可能会导致很多碎片产生,建议用字段表示,而不是直接删除,这样高并发下,新增数据性能以及删除数据性能都会比较高,避免频繁合并和分裂
哈希索引
在mysql中,只有memory存储引擎支持显示的哈希索引
关键字key,经过哈希算法hash(key)后,产生一个精确的结果值
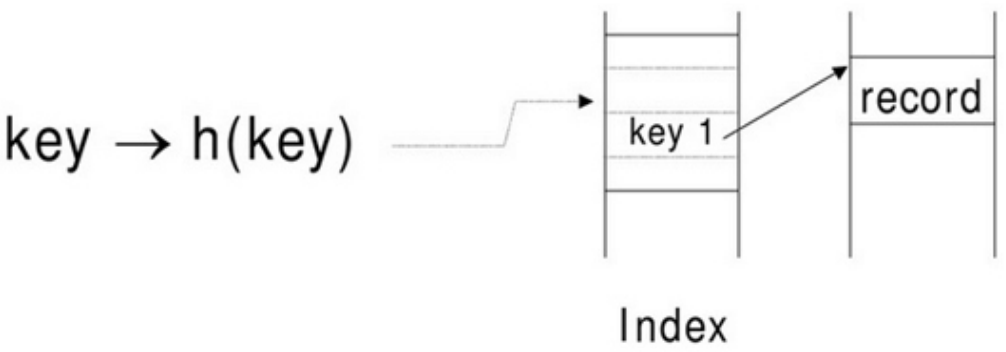
如果有多个关键字相同 产生的hash值也是相同的 有多个重复相同key 会把值放在同一个链表里面,在扫描到这个key的时候就会把链表里的值全部都去取出来
哈希索引和B+树索引的区别:
-
先看下逻辑区别
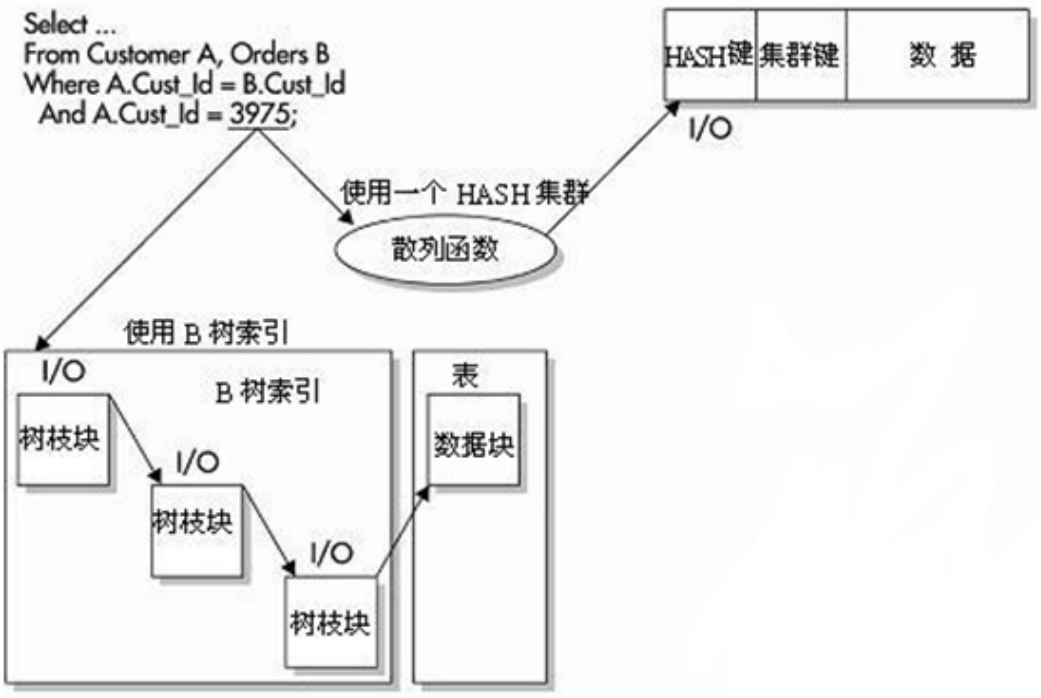
索引优点
1.加快数据检索效率
2.可以创建唯一性约束索引,保证数据库中每一行数据的唯一性
3.加速表和表连接效率
4.在使用分组和排序子句进行数据检索时,可以显著减少查询中分组和排序的时间
索引缺点
1.索引需要占用更多物理存储空间
2.当对表中的数据进行增加,删除和修改的时候,索引野要更新维护,降低了数据维护效率
哪些情况下建议创建索引
-
经常需要搜索的列
-
作为主键的列,有唯一约束索引
-
经常用在表连接的列
-
经常需要排序的列
-
经常使用再where字句中的列
-
经常需要排序/分组的列
哪些情况下不建议创建索引
很不经常被搜索的列
基数值很低的列
长text、blob类型列
唯一索引(约束)(unique key, UNIQUE Index Constraints)
联合索引 Combined Indexes,Multiple-Column Indexes
外键/约束(FIREUGN KEY Constraints)